Геометрия. 7 класс. Глава IV. Параграф 2. Тест 2. 

Вариант I.

1. Проволоке длиной 12 см хотят придать форму равнобедренного треугольника.

В каких случаях (1-4) это невозможно?

1) если боковая сторона 3 см;

2) если основание 3 см;

3) если боковая сторона 5 см;

4) если основание 7 см.

A) 1), 4); B) 1), 3); C) 1), 2); D) 4).

2. На сторонах АВ и АС треугольника АВС отмечены точки К и F, причём точка К является серединой стороны АВ, KF=1 см, AF=12 см. Запишите наибольшее возможное целое значение длины стороны АВ.

A) 27 см; B) 26 см; C) 25 см; D) 24 см.

     

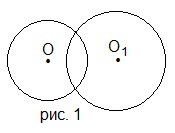
3. Радиусы окружностей, изображенных на рисунке 1, равны 4 см и 5 см. Какой длины может быть отрезок ОО₁?

A) 11 см; B) 10 см; C) 9 см; D) 8 см.

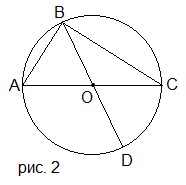
4. Используя данные рисунка 2 доказать, что OB<0,5(AB+BC).

 

Вариант II.

1. Проволоке длиной 8 см хотят придать форму равнобедренного треугольника.

В каких случаях (1-4) получится это сделать?

1) если основание 4 см;

2) если боковая сторона 3 см;

3) если боковая сторона 2 см;

4) если боковая сторона 4 см.

A) 2), 4); B) 2); C) 1), 3); D) 3).

2. На сторонах АС и ВС треугольника АВС отмечены точки D и F, причём точка D является серединой стороны АC, DF=2 см, AF=12 см. Запишите наибольшее возможное целое значение длины стороны АС.

A) 27 см; B) 26 см; C) 25 см; D) 24 см.

3. Радиус большей окружности на рисунке 1 равен 6 см.

ОО₁ = 11 см. Каким числом не может выражаться радиус меньшей окружности?

A) 6 см; B) 9 см; C) 5 см; D) 7 см.

   

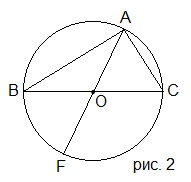
4. Используя данные рисунка 2 доказать, что OА<0,5(AB+АC).

 

Вариант III.

1. Выяснить, существует ли треугольник со сторонами:

1) 1,3 см; 2,1 см и 3,4 см;

2) 2 см, 3 см и 4 см;

3) 1 см, 1 см и 6 см;

4) 1 см, 2 см и 3 см;

5) 5 см, 6 см и 7 см.

В ответе указать номер(а) существующего треугольника.

A) 3), 5); B) 2), 5); C) 2), 3); D) 5).

2. Дан треугольник АВС с целочисленными сторонами. Точка М – середина отрезка АВ.

Точка К лежит на стороне ВС, причём МК=3 см, АК=8 см. Найдите все возможные значения длины отрезка АВ.

A) 11≤AB≤21; B) 9≤AB≤15;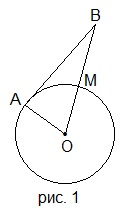     

C) 11<AB<21; D) 12≤AB≤22.

3. На рисунке 1 АВ=15 см, АО=6 см. Каким числом не может выражаться длина отрезка ВМ?

A) 4 см; B) 9 см; C) 14 см; D) 15 см.

4. В треугольнике АВС (AB<BC) ВМ – медиана. Докажите, что BM>0,5(BC-AB).

Указание. Продлите медиану ВМ за точку М на отрезок МЕ=ВМ. К треугольнику ВСЕ примените следствие к теореме «Неравенство треугольника»: каждая сторона треугольника больше разности двух других сторон. Рассмотрите треугольники АВМ и СЕМ.

 

Вариант IV.

1. Выяснить, существует ли треугольник со сторонами:

1) 2 см; 4 см и 6 см;

2) 3,5 см, 6 см и 10 см;

3) 3 см, 4 см и 5 см;

4) 1 см, 5 см и 5 см;

5) 2 см, 2 см и 5 см.

В ответе указать номер(а) существующего треугольника.

A) 3), 5); B) 2), 3); C) 3), 4); D) 1), 3).

2. Дан треугольник АВС с целочисленными сторонами. Точка М – середина отрезка АВ.

Точка К лежит на стороне ВС, причём МК=2 см, АК=6 см. Найдите все возможные значения длины отрезка АВ.

A) 11≤AB≤21; B) 9≤AB≤15;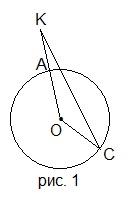   

C) 9<AB<15; D) 10≤AB≤16.

3. На рисунке 1 СК=13 см, ОС=4 см. Каким числом не может выражаться длина отрезка АК?

A) 7 см; B) 6 см; C) 5 см; D) 8 см.

4. В треугольнике АВС (AB<АC) АК – медиана. Докажите, что АК>0,5(АC-AB).

Указание. Продлите медиану АК за точку К на отрезок МК=АК. К треугольнику АСМ примените следствие к теореме «Неравенство треугольника»: каждая сторона треугольника больше разности двух других сторон. Рассмотрите треугольники АВК и МСК.